NMR shielding constants through polarizable embedding. Part II

In my previous post on the subject of NMR shieldings in polarizable embedding, some progress has been made.

Through the polarizable embedding (PE) approach, calculating gauge-independent magnetic properties in the electrostatic field of the surroundings is now possible. Currently, the PE approach supports an electrostatic multipole expansion up to (and including) order 5, where order 0 is a charge, order 1 is a dipole and so on. The magnetic properties can now be calculated with contributions from quadrupoles (order 2), but we expect to finish the rest of the contributions once some development time is available from the Gen1Int-developers.

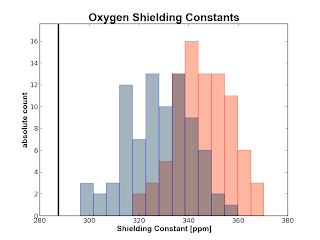
If you have a water cluster and you calculate the shielding constants for the Oxygen and the Hydrogens of the central water molecule with some surrounding water molecules also treated with quantum mechanics, you can now obtain plots like the following

 

The plots are obtained from 50 snapshots from an MD of water in water. The black vertical line is the experimental number obtained from a (somewhat) recent paper by Kongsted et al. The red histogram is made from numbers calculated at the B3LYP/pcS-0 level of theory whereas the blue histograms are calculated on the same geometry with B3LYP/pcS-1. The gray color in the oxygen plot around the experimental value depicts the uncertainty in that result.

Since this is not going to be a paper on benchmarking your top 20 functionals with your top 5 basis sets, we will from now probably use the KT3 functional with some flavour of the Frank Jensen pcS-n basis sets.

edit 1: Updated the plots to show transparency so you can see both distributions.

edit 2: Added the following based on feedback in the comments to the original post

Janus Eriksen suggested using KT1 or KT2 instead of KT3 since we were only interested in shielding constants. I personally think that Magnus wrote a reasonable response indicating that the difference in using KT1, KT2 and K3 is likely less than 1 ppm in error, but the switch from B3LYP would likely decrease the error by about 13 ppm.

Anders Steen Christen had a valid point in suggesting that we cannot really use the MD-simulations to compare to experiment because the shielding tensors are extremely sensitive to the geometry of the water molecules. Since I haven't really written anything about what we actually aim to do with the data in the end, the point is moot in that respect, but it is a strong point. Perhaps Coupled-Cluster based MD would be the right thing to do.

I would say that this really proves the strength of blogging about your ideas and getting input from others.