I'm proud to announce the immediate availability of FragIt 1.3!
From the release notes:
* Stabilization of the API for 3rd party uses
* API has support for a QM-region in the XYZ-MFCC
writer. This QM-region can be expanded by including
covalently bound or hydrogen bound neighbours.
This support is slated to be included more generally
in a future fragit 1.4 release series.
* A visually more pleasing color scheme. We are no
longer living in an 8-bit world.
* FragIt now exits more cleanly if it cannot find itself.
The visually more pleasing color scheme was discussed in a previous post.
Monday, December 2, 2013
Friday, November 8, 2013
Calculating Shieldings for Proteins
I'm just going to show some recent work on extending the Polarizable Embedding from being a focused QM/MM model into an approach to generate parameters for entire proteins or DNA. Here is a snapshot of the human protein GB3 (PDB: 2OED) with the central QM-fragment we are interested in - here LYS4 - shown in vdw-spheres. Also in the QM-region are neighbouring residues and stuff (side-chains and water) that binds to the central fragment of interest) all highlighted in cyan in sticks. The rest of the protein along with a lot of water is the MM-region. Only the protein is shown in a classical cartoon rendering.
Enjoy
Enjoy
Wednesday, October 30, 2013
FragIt has a better look!
Active development with FragIt is still going strong as I work my way through interfacing it with other software that we are building in-house to allow you to run these high-quality QM/MM calculations with relative ease.
I've just added a visually more pleasing color scheme to the development version which you can see in the image below
The old colorscheme is to the left and the new is to the right.
it just became a lot cooler to visually inspect your molecule of interest.
I've just added a visually more pleasing color scheme to the development version which you can see in the image below
The old colorscheme is to the left and the new is to the right.
it just became a lot cooler to visually inspect your molecule of interest.
Friday, October 18, 2013
Release of FragIt 1.2
After a ferocious development spree, I am proud to announce the release of FragIt 1.2.
Under the hood, it has primarily been reworking some of the finer details of the API to allow for better integration with programs wishing to use it.
Directly from the release-notes:
FragAway!
Under the hood, it has primarily been reworking some of the finer details of the API to allow for better integration with programs wishing to use it.
Directly from the release-notes:
This release provides Molcular Fragmentation with Conjugate Caps (MFCC) support through FragIt. Currently, it dumps all capped fragments and all caps as separate .xyz files so you can process them further on in the quantum chemistry code of your choice. You can access it through thewriter = XYZ-MFCCoption in the[fragmentation]group.
This release also includes some updated API for better integration with other codes that wants to interface with FragIt.
FragAway!
Friday, August 23, 2013
Be careful when you extrapolate to the complete basis set limit!
In our soon-to-be-finised manuscript on shielding constants obtained through the QM/MM with the MM-region described by a high-quality polarizable embedding potential (PE), I've done a thing I should have done a while ago. But, as it is always the case with these things, you end up doing it in the wrong order.
How do you continue from these values to an estimate of the basis set limit at infinity? According to Jans blog post, you should fit your data according to
$$
Y(l_{max}) = Y_{CBS} + a \cdot e^{b \cdot l_{max}}
$$
to get the most accurate result. I have done so in using WolframAlpha and I have obtained the following plot (blue dashed line) with $Y_{CBS}=-176.5$ ppm.
"That is a terrible fit!", I can hear you say. And indeed it is. What is going on? It turns out (and please give me some references if you know them!) that the pcS-0 results are actually too bad to be taken seriously. The single zeta basis set is not enough to even get a qualitatively correct description of that wave function, i.e. what you get is just wrong. If you remove that point you get the solid blue curve which is a really good fit with $Y_{CBS}=-187.7$ ppm.
If you want to use the alternative extrapolation scheme that Jan provides, i.e.
$$
Y(l_{max}) = Y_{CBS} + b\cdot l_{max}^{-3}
$$
one obtains the red solid curve with $Y{CBS}=-182.9$ ppm which 5 ppm off from the exponential fit.
As Frank (and Grant) are commenting below, one should not trust numbers from SZ basis sets and +Anders Steen Christensen noted that even the DZ results could/should be disregarded. The only problem is that the size of my calculations are increasing, and a 5Z calculation is pretty much out of reach beyond the TZ basis set. Jans post does mention that one should use a DZ quality basis set, shame on me I guess for even trying with pcS-0.
Just be careful out there and remember to extrapolate!
edit1: fixed the last formula
edit2: Frank Jensen has given a lengthy comment on the matter which gives a lot of insigth. Read it below. I've added some clarifying text here and there based on his comments and will likely follow up on it in a later blog post.
I read the blogpost on basis set extrapolation by +Jan Jensen and thought I should try. Here is what I got by calculating the shielding constants for oxygen-17 in acrolein using KT3/pcS-n//B3LYP/aug-cc-pVDZ solvated by a 12 Å sphere of explicit water molecules described by the PE potential.
| pcS-0 | pcS-1 | pcS-2 | pcS-3 |
|---|---|---|---|
| -309.2 | -216.9 | -191.6 | -188.2 |
How do you continue from these values to an estimate of the basis set limit at infinity? According to Jans blog post, you should fit your data according to
$$
Y(l_{max}) = Y_{CBS} + a \cdot e^{b \cdot l_{max}}
$$
to get the most accurate result. I have done so in using WolframAlpha and I have obtained the following plot (blue dashed line) with $Y_{CBS}=-176.5$ ppm.
"That is a terrible fit!", I can hear you say. And indeed it is. What is going on? It turns out (and please give me some references if you know them!) that the pcS-0 results are actually too bad to be taken seriously. The single zeta basis set is not enough to even get a qualitatively correct description of that wave function, i.e. what you get is just wrong. If you remove that point you get the solid blue curve which is a really good fit with $Y_{CBS}=-187.7$ ppm.
If you want to use the alternative extrapolation scheme that Jan provides, i.e.
$$
Y(l_{max}) = Y_{CBS} + b\cdot l_{max}^{-3}
$$
one obtains the red solid curve with $Y{CBS}=-182.9$ ppm which 5 ppm off from the exponential fit.
As Frank (and Grant) are commenting below, one should not trust numbers from SZ basis sets and +Anders Steen Christensen noted that even the DZ results could/should be disregarded. The only problem is that the size of my calculations are increasing, and a 5Z calculation is pretty much out of reach beyond the TZ basis set. Jans post does mention that one should use a DZ quality basis set, shame on me I guess for even trying with pcS-0.
Just be careful out there and remember to extrapolate!
edit1: fixed the last formula
edit2: Frank Jensen has given a lengthy comment on the matter which gives a lot of insigth. Read it below. I've added some clarifying text here and there based on his comments and will likely follow up on it in a later blog post.
Saturday, August 3, 2013
What is it with this linear scaling stuff anyway?
Enormous amounts of research time has gone into researching computational methods that are linear scaling with respect to the system size. That is, double the size of your system and you only double the computation time. If just all methods were as such, the queue on your local super computer cluster would be easier to guess when computers were available instead of seeing a wall of 200+ hours of jobs just sitting there because people don't give a crap.
Inspired by +Jan Jensen and a recent blog post of his (which I was reminded of when I wrote another blog post on the subject of many-body expansions), I set out to actually do the calculations on timings myself albeit with a different goal in mind.
2-body calculations
Even if you use the many-body expansion of the energy, I showed that the accumulated number of calculations one would need increases dramatically for large N-body. If we only focus on doing one- and two-body calculations, the effect is barely visible in the previous plot, but calculating the computational time from Jan's linear model (only do nearest neighbors) together with one where we do all pairs, we see that even at the two-body level, there is no linear scaling unless you do some approximations.
Here, I have assumed a computational scaling of $\alpha=2.8$ and uniform monomer sizes. I've assumed that a monomer calculation takes 1s and there is no overhead nor interaction at the monomer level.
Admittedly, the linear model is crude, but it shows the best scaling you could hope for by including the minimum amount of two-body calculations. In a more realistic case, you would end up somewhere between the red and the black line, but that is the subject for a future post.
This is why we need linear scaling!
3-body calculations
Just for the fun of it, here is the 3-body scaling
and I dare not think of what the time would be for the calculation without approximations for higher n-body calculations.
I think that we can all agree on that approximations must be made or else we are doomed.
We need linear scaling!
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Inspired by +Jan Jensen and a recent blog post of his (which I was reminded of when I wrote another blog post on the subject of many-body expansions), I set out to actually do the calculations on timings myself albeit with a different goal in mind.
2-body calculations
Even if you use the many-body expansion of the energy, I showed that the accumulated number of calculations one would need increases dramatically for large N-body. If we only focus on doing one- and two-body calculations, the effect is barely visible in the previous plot, but calculating the computational time from Jan's linear model (only do nearest neighbors) together with one where we do all pairs, we see that even at the two-body level, there is no linear scaling unless you do some approximations.
Admittedly, the linear model is crude, but it shows the best scaling you could hope for by including the minimum amount of two-body calculations. In a more realistic case, you would end up somewhere between the red and the black line, but that is the subject for a future post.
This is why we need linear scaling!
3-body calculations
Just for the fun of it, here is the 3-body scaling
I think that we can all agree on that approximations must be made or else we are doomed.
We need linear scaling!
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Wednesday, July 31, 2013
would you do FMO-10 if you could?
The many-body expansion of the energy is a popular way to reduce the cost of computing the energy of an entire system too large to fit into your computer. The strategy is quite simple: chop your large system into several small pieces, do your quantum mechanics on each piece. In practice you can stop here (1-body), but often people to pair-corrections (2-body) to get good results and triples-corrections (3-body) if they want to be fancy. There are many implementations of this, including the eXplicit-POLarization method, the Fragment Molecular Orbtital method and the electrostatically-embedded many-body method, just to name a few.
My question is: would you do a 10-body calculation if you could?
Here is an argument against it, and it does not involve anything to do with accuracy, but rather computational cost.
The number of n-mers (1-mers, 2-mers, 3-mers and so on) increase quite drastically if one does not include approximations, but I can hear you ask: how bad is it?
For 16 water molecules, each water molecule is a 1-mer, the total number of calculations one would need to perform in order to calculate the n-body calculation is presented in the figure below
where we see that a 10-body calculation would require a total 58650 unique calculations whereas the 3-body calculation would require a "mere" 696.
Edit: For a discussion about timings, +Jan Jensen wrote a blog post on the subject.
That's at least an argument against dreaming of large n-body calculations unless you severely sit down and think about eliminating some of these calculations.
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
My question is: would you do a 10-body calculation if you could?
Here is an argument against it, and it does not involve anything to do with accuracy, but rather computational cost.
The number of n-mers (1-mers, 2-mers, 3-mers and so on) increase quite drastically if one does not include approximations, but I can hear you ask: how bad is it?
For 16 water molecules, each water molecule is a 1-mer, the total number of calculations one would need to perform in order to calculate the n-body calculation is presented in the figure below
where we see that a 10-body calculation would require a total 58650 unique calculations whereas the 3-body calculation would require a "mere" 696.
Edit: For a discussion about timings, +Jan Jensen wrote a blog post on the subject.
That's at least an argument against dreaming of large n-body calculations unless you severely sit down and think about eliminating some of these calculations.
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Sunday, July 21, 2013
Oxygen, you little rascal! Part 2.
Background
In the ongoing saga (read part I) with acrolein solvated in water, we were having problems with our high quality embedding potential just not converging nicely when increasing system sizes, QM-region sizes. We were using a functional to get good shielding constants (the KT3 functional) with a basis set designed to get good shielding constants (the apcS-1 basis set) but no matter what tried, the widely adopted TIP3P potential for water just did it better than we did. And we were just confused!
Solution
The problem turned out to be the basis set that with the diffuse functions leaked electron density out into the MM-region when using the PE potential and this was causing some disturbance with the induced dipoles. On the contrary, our belief is that TIP3P is a much too soft potential and there is a large degree of error cancellation because of that. Both are effects I would think to be very small and have no real impact but I had also forgotten that we were talking about nuclear shielding constants which are sensitive as f*ck the wave function.
I switched to the smaller pcS-1 basis set and all that leaking-trouble went away. Everything that we did not expect was gone. TIP3P was converging rather slowly and the PE-model was quickly converging as is shown below for an average of 120 snapshots.
The PE numbers (blue) are converged at QM size 3 but even size 1 and 2 show some good indications. For size 1, acrolein is solvated in purely classical water. As we would expect, the improved potential means that we are converging (fast) towards a value for the absolute shielding of acrolein in water valued -223.2 ppm.
Outlook
We will return to the use of diffuse basis functions and a proper quantum mechanical fix in a later paper as this work here sparked my co-worker +Jógvan Magnus Haugaard Olsen into actually picking up work he had done on repulsion during his Ph.D. (pdf of his thesis)
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Friday, June 21, 2013
Oxygen, you little rascal!
Calculations of NMR shielding constants using my recent DFT-PE implementation has been underway for some time and I wanted to share the latest results. DFT-PE is a QM/MM type method where the MM region is treated by a polarizable force field calculated for that particular geometry. Initially, I just went away and calculated the NMR shielding constants for acrolein and a few waters with QM and as large an MM region as I could possibly cut out. Unfortunately, the results looked a bit weird when we compared them to a non-polarizable force field (TIP3P) of lesser quality. Lesser in the sense that the description of the electrostatic potential from TIP3P does not match that of the QM electrostatic potential (magnus paper?).
The problem was that the TIP3P results seemed to converge really fast with respect to the size of the QM region and I, using a high-quality PE potential, was converging slower. I went back to the drawing board and came up with the following analysis
Here we see that for increasing sizes of QM region (red) the NMR shielding constant of 17O is reduced by 102 ppm going from acrolein in the gas phase to acrolein surrounded by 53 water molecules (follow the diagonal). Going vertically up in each row, we decrease the size of the QM region, gradually replacing QM waters with MM waters (blue). Deviations from the QM result for that particular system size is shown below each illustration.
Acrolein in 53 MM waters deviates by 23.3 ppm compared to the full QM calculation. This deviation is (if the polarizable force field we are using) purely quantum mechanical. If the first solvation shell is included, that is 7 QM waters, the deviation drops to 4.3 ppm and only improves from here.
Needless to say, TIP3P is also doing great here, but the convergence is not nearly as systematic as is observed for PE. So, it looks like the PE potential is doing it wrong for the right reasons, where as TIP3P is right for the wrong reasons ... that is, using DFT with TIP3P, two wrongs does make a right!
Final note: Oxygen is really, really hard to get right. I showed you only the most difficult case I tried – NMR shielding constants for the rest of acrolein are converged much faster using the smaller QM regions shown above. Luckily for later studies on proteins, nobody does that silly Oxygen atom anyways.
This work is licensed under a Creative Commons Attribution 3.0 Unported License.
Monday, June 10, 2013
FragIt and Metals
FragIt is a tool that helps you setup a fragment calculation, more specifically for use in the Fragment Molecular Orbital (FMO) method and its Testosterone induced cousin the Effective Fragment Molecular Orbital (EFMO) method.
Since my switch to the University of Southern Denmark, FragIt's capabilities have grown a bit. Now it supports Molecular Fragmentation with Conjugate Caps so it can dump coordinate files and you can estimate interaction energies quickly and I am trying to switch to a more flexible configuration system, but that is a topic for another post on a related blog.
However, my proudest moment regarding FragIt must have been today when I finally fixed an issue with FragIt that has been haunting me for some time. Metal ions. The problem is that FragIt uses the excellent Open Babel toolkit as its underlying work horse, but the charge models that are implemented are misbehaving when metals are present (through the Python bindings). The partial charges are not present for the metals which I guess makes sense
My solution was rather elegant:
while metals are present
The only catch is that whatever metal ions you want to include has to be last in whatever structure file you are using and I should mention that the web interface is not yet updated with this feature.
That's what conferences are for! Stay tuned for a 1.0.7 point release sometime in the near future.
btw - metal ions can be mispelled to say meta lions which I at this hour find rather amusing.
Since my switch to the University of Southern Denmark, FragIt's capabilities have grown a bit. Now it supports Molecular Fragmentation with Conjugate Caps so it can dump coordinate files and you can estimate interaction energies quickly and I am trying to switch to a more flexible configuration system, but that is a topic for another post on a related blog.
However, my proudest moment regarding FragIt must have been today when I finally fixed an issue with FragIt that has been haunting me for some time. Metal ions. The problem is that FragIt uses the excellent Open Babel toolkit as its underlying work horse, but the charge models that are implemented are misbehaving when metals are present (through the Python bindings). The partial charges are not present for the metals which I guess makes sense
My solution was rather elegant:
while metals are present
- store a copy of them in a separate list
- delete them from the system
- calculate the partial charges of the system without the metal ions.
The only catch is that whatever metal ions you want to include has to be last in whatever structure file you are using and I should mention that the web interface is not yet updated with this feature.
That's what conferences are for! Stay tuned for a 1.0.7 point release sometime in the near future.
btw - metal ions can be mispelled to say meta lions which I at this hour find rather amusing.
Wednesday, April 24, 2013
Visualizing a lot of FMO PIEDA numbers. Part II
In the last post on the subject of FMO PIEDA numbers, there were some issues with the fragmentation that did not match between two different snapshots in the same reaction trajectory.
I fixed that fragmentation problem, ran the numbers again and it looks like some neat stuff can be extracted.
Remember that the structures are generated using PM6 with MOZYME enabled and that energy-refinement of the barrier is done at the FMO2/6-31G(d)/PCM level of theory. The CON structures have some part of the structure constrained (far away from the active site) and the UCO structures are allowed to fully relax. The problem still looks like this
To tease you with some data, here is a table from a short write-up I did. Column two and three represents the difference in energy (by the method in the first column) between the TS and the reactant. The last column is the energy difference between column two and three. The first row is thus the difference in sum of one-body energies, second row is difference in the sum of fragment interaction energies (FIEs) and the last row is the difference in total FMO2 energy.
The one-body case is a solved case because inspection reveals that the internal energies of the substrate contributes +3.5 kcal/mol, ASP119 contributes +5.3 kcal/mol and ASN35 contributes -4.3 kcal/mol which when summed up is roughly the 4 kcal/mol we need. The rest is just internal re-arrangement that eventually cancels out.
The problem with the barrier height, however, is that at the two-body level (second row), the CON structures provide almost 4 kcal/mol worth of stabilization whereas the UCO structures are destabilized by 18.6 kcal/mol. It would be natural to investigate what happens if we look at the FIEs between the substrate and the entire enzyme. This looks like the following
what is curious is that we see distinct peaks - the largest (positive) peak can be attributed to an interaction with ARG112, but if we sum all IEFs up they amount to +0.5 kcal/mol which is very far from the +18.6 we are trying to account for. The conclusion is (currently) that because the protein is allowed to fully relax, many small contributions amount to the 18.6.
credits to this sites table-generator because I lost all my HTML skills whilst fighting FORTRAN
I fixed that fragmentation problem, ran the numbers again and it looks like some neat stuff can be extracted.
Remember that the structures are generated using PM6 with MOZYME enabled and that energy-refinement of the barrier is done at the FMO2/6-31G(d)/PCM level of theory. The CON structures have some part of the structure constrained (far away from the active site) and the UCO structures are allowed to fully relax. The problem still looks like this
To tease you with some data, here is a table from a short write-up I did. Column two and three represents the difference in energy (by the method in the first column) between the TS and the reactant. The last column is the energy difference between column two and three. The first row is thus the difference in sum of one-body energies, second row is difference in the sum of fragment interaction energies (FIEs) and the last row is the difference in total FMO2 energy.
| dE(1,5)_con | dE(1,5)_uco | ddE(uco-con) | |
|---|---|---|---|
| FMO1-MP2/6-31G(d)/PCM | 25.4 | 29.4 | 4.0 |
| $\sum_{IJ} \Delta E^{MP2}_{IJ}$ | -3.7 | 18.6 | 22.4 |
| FMO2-MP2/6-31G(d)/PCM | 25.9 | 55.0 | 29.1 |
The one-body case is a solved case because inspection reveals that the internal energies of the substrate contributes +3.5 kcal/mol, ASP119 contributes +5.3 kcal/mol and ASN35 contributes -4.3 kcal/mol which when summed up is roughly the 4 kcal/mol we need. The rest is just internal re-arrangement that eventually cancels out.
The problem with the barrier height, however, is that at the two-body level (second row), the CON structures provide almost 4 kcal/mol worth of stabilization whereas the UCO structures are destabilized by 18.6 kcal/mol. It would be natural to investigate what happens if we look at the FIEs between the substrate and the entire enzyme. This looks like the following
what is curious is that we see distinct peaks - the largest (positive) peak can be attributed to an interaction with ARG112, but if we sum all IEFs up they amount to +0.5 kcal/mol which is very far from the +18.6 we are trying to account for. The conclusion is (currently) that because the protein is allowed to fully relax, many small contributions amount to the 18.6.
credits to this sites table-generator because I lost all my HTML skills whilst fighting FORTRAN
Tuesday, April 16, 2013
DALTON mol File Input Generator for Open Babel
Because of my new engagement with DALTON, I felt there was a serious lack of availability in the open source tool chain that I am used to: There is no input file generator in Open Babel for DALTON, until now.
Through a series of commits in my own fork of the official Open Babel repository, I've added a basic mol file input generator (and reader too!). The commits have been marked with a pull request to be merged into the official repository, but it looks like it is only updated every now and then. If you want to get all crazy right away, clone my repository and get cracking.
Experienced users with DALTON knows that there are two input files. the molecule file and the DALTON input file (dal file). The mol file contains the coordinates of the atoms, their charge and the basis set for the computation. The dal file tells DALTON what to actually do with the content of the mol file. Thus, the dal file is about the quantum chemistry which is traditionally left out in Open Babel and I've only focused on getting the mol-file ready - most users of DALTON use a single dal file anyways and use different mol files. I guess my own scripts to make easy conversions to and from DALTON are now void (at least partially).
Hooray for Open Source!
Addendum: I should mention that coordinates can also be extracted from DALTON log files. As I myself do not (usually) have a need beyond coordinate extractions I will leave it as is for now.
Through a series of commits in my own fork of the official Open Babel repository, I've added a basic mol file input generator (and reader too!). The commits have been marked with a pull request to be merged into the official repository, but it looks like it is only updated every now and then. If you want to get all crazy right away, clone my repository and get cracking.
Experienced users with DALTON knows that there are two input files. the molecule file and the DALTON input file (dal file). The mol file contains the coordinates of the atoms, their charge and the basis set for the computation. The dal file tells DALTON what to actually do with the content of the mol file. Thus, the dal file is about the quantum chemistry which is traditionally left out in Open Babel and I've only focused on getting the mol-file ready - most users of DALTON use a single dal file anyways and use different mol files. I guess my own scripts to make easy conversions to and from DALTON are now void (at least partially).
Hooray for Open Source!
Addendum: I should mention that coordinates can also be extracted from DALTON log files. As I myself do not (usually) have a need beyond coordinate extractions I will leave it as is for now.
Wednesday, April 10, 2013
NMR shielding constants through polarizable embedding. Part II
In my previous post on the subject of NMR shieldings in polarizable embedding, some progress has been made.
Through the polarizable embedding (PE) approach, calculating gauge-independent magnetic properties in the electrostatic field of the surroundings is now possible. Currently, the PE approach supports an electrostatic multipole expansion up to (and including) order 5, where order 0 is a charge, order 1 is a dipole and so on. The magnetic properties can now be calculated with contributions from quadrupoles (order 2), but we expect to finish the rest of the contributions once some development time is available from the Gen1Int-developers.
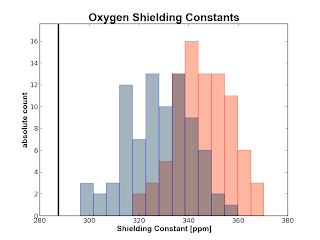
If you have a water cluster and you calculate the shielding constants for the Oxygen and the Hydrogens of the central water molecule with some surrounding water molecules also treated with quantum mechanics, you can now obtain plots like the following
The plots are obtained from 50 snapshots from an MD of water in water. The black vertical line is the experimental number obtained from a (somewhat) recent paper by Kongsted et al. The red histogram is made from numbers calculated at the B3LYP/pcS-0 level of theory whereas the blue histograms are calculated on the same geometry with B3LYP/pcS-1. The gray color in the oxygen plot around the experimental value depicts the uncertainty in that result.
Since this is not going to be a paper on benchmarking your top 20 functionals with your top 5 basis sets, we will from now probably use the KT3 functional with some flavour of the Frank Jensen pcS-n basis sets.
edit 1: Updated the plots to show transparency so you can see both distributions.
edit 2: Added the following based on feedback in the comments to the original post
Janus Eriksen suggested using KT1 or KT2 instead of KT3 since we were only interested in shielding constants. I personally think that Magnus wrote a reasonable response indicating that the difference in using KT1, KT2 and K3 is likely less than 1 ppm in error, but the switch from B3LYP would likely decrease the error by about 13 ppm.
Anders Steen Christen had a valid point in suggesting that we cannot really use the MD-simulations to compare to experiment because the shielding tensors are extremely sensitive to the geometry of the water molecules. Since I haven't really written anything about what we actually aim to do with the data in the end, the point is moot in that respect, but it is a strong point. Perhaps Coupled-Cluster based MD would be the right thing to do.
I would say that this really proves the strength of blogging about your ideas and getting input from others.
Through the polarizable embedding (PE) approach, calculating gauge-independent magnetic properties in the electrostatic field of the surroundings is now possible. Currently, the PE approach supports an electrostatic multipole expansion up to (and including) order 5, where order 0 is a charge, order 1 is a dipole and so on. The magnetic properties can now be calculated with contributions from quadrupoles (order 2), but we expect to finish the rest of the contributions once some development time is available from the Gen1Int-developers.
If you have a water cluster and you calculate the shielding constants for the Oxygen and the Hydrogens of the central water molecule with some surrounding water molecules also treated with quantum mechanics, you can now obtain plots like the following
Since this is not going to be a paper on benchmarking your top 20 functionals with your top 5 basis sets, we will from now probably use the KT3 functional with some flavour of the Frank Jensen pcS-n basis sets.
edit 1: Updated the plots to show transparency so you can see both distributions.
edit 2: Added the following based on feedback in the comments to the original post
Janus Eriksen suggested using KT1 or KT2 instead of KT3 since we were only interested in shielding constants. I personally think that Magnus wrote a reasonable response indicating that the difference in using KT1, KT2 and K3 is likely less than 1 ppm in error, but the switch from B3LYP would likely decrease the error by about 13 ppm.
Anders Steen Christen had a valid point in suggesting that we cannot really use the MD-simulations to compare to experiment because the shielding tensors are extremely sensitive to the geometry of the water molecules. Since I haven't really written anything about what we actually aim to do with the data in the end, the point is moot in that respect, but it is a strong point. Perhaps Coupled-Cluster based MD would be the right thing to do.
I would say that this really proves the strength of blogging about your ideas and getting input from others.
Monday, April 8, 2013
Visualizing a lot of FMO PIEDA numbers. A Preliminary look.
I've assisted in calculating some energy refinements using FMO2-MP2/PCM/6-31G(d) on top of a colleagues proposed trajectory calculated using PM6//MOZYME for part of the reaction step of Bacillus circulans xylanase. Two versions of this path was produced. One with constraints on some part of the structure (CON) and one without constraints (UCO). They are shown here
This FMO2 barrier is quite unrealistic, especially the unconstrained one so what is cause this large reaction barrier?
To investigate this, we are trying to run some PIEDA calculations to figure out which pairs are interacting strongly (and perhaps differently). PIEDA gives you an energy decomposition analysis of the individual pairs in an FMO calculation. So we get electrostatic contributions, exchange-repulsion, charge-transfer (and what is left), dispersion and solvation energy too.
The BCX-system we are looking at currently has 302 fragments (a total of 3172 atoms) which is actually the whole protein and its substrate. That means you get 45451 unique pairs and each pair is decomposed into five different terms giving you a wonderful 227255 numbers you have to visualize somehow. I haven't really figured out how to do this in a nice way, so instead I will plot the the total interaction energies between each unique pair of fragment for snapshot 2 and 3 for the blue curve (UCO) in the above graph.
I discovered the problem ... the fragmentation was not exactly the same along the entire UCO path which of course will make everything break down. Back to the drawing board then. What gave it away? Look here at the difference in pair-energies between frame 0 and frame 5 (click to see it in its full size - hell even that does not justify it)
So there it is. An unrealistic result can be your own fault no matter how hard you actually try to convince yourself that you used the same scripts for both runs.
This FMO2 barrier is quite unrealistic, especially the unconstrained one so what is cause this large reaction barrier?
I discovered the problem ... the fragmentation was not exactly the same along the entire UCO path which of course will make everything break down. Back to the drawing board then. What gave it away? Look here at the difference in pair-energies between frame 0 and frame 5 (click to see it in its full size - hell even that does not justify it)
So there it is. An unrealistic result can be your own fault no matter how hard you actually try to convince yourself that you used the same scripts for both runs.
Sunday, April 7, 2013
Building the OpenChemistry Packages on Ubuntu 12.04
Inspired by the latest Google+ posts by several of the developers of Avogadro (+Marcus Hanwell, +David Lonie, +Open Chemistry) I decided to install what is now known as Avogadro2 along with several other Open Chemistry packages.
The first step was to get hold of the sources which proved to be easy.
Second step was to compile which was also quite easy because the new cmake scripts downloads the correct packages you need (clever!). However, on my Ubuntu 12.04 I had to install the following extra packages to get rolling - my approach was to just see what failed and install what was missing.
sudo apt-get install libxt-dev
sudo apt-get install libqt4-opengl-dev
sudo apt-get install libbz2-1.0 libbz2-dev libbz2-ocaml libbz2-ocaml-dev
sudo apt-get install libqt4-dev qt4-dev-tools libqt4-webkit libqt4-core libqtwebkit-dev qt4-designer
Now, I haven't run the make install part of the whole shebang yet, but I have been able to run the new Avogadro application directly from the build directory so at least everything seems to compile fine. I was very inspired by the post on python input generators by David Lonie. Maybe I'll cook something up some day.
For now, it seems that Avogadro2 is a step back in terms of what you can actually do, but it also appears the developers are hard at work actually getting the application up to speed and ready for a beta-release very soon. I know I am excited.
The first step was to get hold of the sources which proved to be easy.
Second step was to compile which was also quite easy because the new cmake scripts downloads the correct packages you need (clever!). However, on my Ubuntu 12.04 I had to install the following extra packages to get rolling - my approach was to just see what failed and install what was missing.
sudo apt-get install libxt-dev
sudo apt-get install libqt4-opengl-dev
sudo apt-get install libbz2-1.0 libbz2-dev libbz2-ocaml libbz2-ocaml-dev
sudo apt-get install libqt4-dev qt4-dev-tools libqt4-webkit libqt4-core libqtwebkit-dev qt4-designer
Now, I haven't run the make install part of the whole shebang yet, but I have been able to run the new Avogadro application directly from the build directory so at least everything seems to compile fine. I was very inspired by the post on python input generators by David Lonie. Maybe I'll cook something up some day.
For now, it seems that Avogadro2 is a step back in terms of what you can actually do, but it also appears the developers are hard at work actually getting the application up to speed and ready for a beta-release very soon. I know I am excited.
Monday, April 1, 2013
Extending FragIt for Molecular Fragmentation with Conjugate Caps
As the co-author of FragIt(web, code), a piece of
software written in Python using the Open Babel API, to help setup
and fragment large molecules in fragment based methods, I have to
return to this (excellent) piece of software to make it work with
Molecular Fragmentation with Conjugate Caps (MFCC) methods which is
the approach that my new work-place has taken as their method of
choice in fragment based methods. Currently, FragIt only (officially)
supports the Fragment Molecular Orbital (FMO) method.
Step I of this transformation is to
realize that FMO and MFCC are two very different beasts. While the
theory of FMO is more hairy, the information that FMO needs to run is
vastly less than MFCC. In FMO, you specify pairs of atoms between
which you wish to fragment and then everything goes along nicely
whereas in MFCC you build fragments, attach caps and build extra
fragments from those caps (called conjugate caps). The latter is very
tough to do generally which is the approach and idea of FragIt in the
first place: Mostly because getting the correct SMARTS you need is very
cumbersome. As with the previous approach of FragIt, I'll make it work for proteins by selecting the appropriate SMARTS and program it in such a way that extensions to other systems would be straight-forward by simply figuring out additional patterns.
Right now my approach is to build
“capping”-SMARTS that select atoms around places of fragmentation
and build those caps in Open Babel. Non-trivial task is non-trivial I
must admit.
Stay tuned as I explore the SMARTS and
code needed to accomplish this.
Wednesday, March 27, 2013
NMR shielding constants through polarizable embedding
After I finished my Ph.D. in the Jan Jensen group, I've begun working at the University of Southern Denmark with Jacob Kongsted.
Apart from using DALTON instead of GAMESS I've also switched gears and I am now focused on an advanced form of QM/MM which is called polarizable embedding (see this paywalled link for details). Basically your gas-phase Fock operator is extended with interactions from the surroundings. In the language of polarizable embedding (PE) we constructs the effective Fock operator here for Hartree-Fock
$\hat{f}_{eff} = \hat{f}_{HF} + \hat{\nu}_{PE}$
The PE is a sum of interactions from the surroundings onto a molecule of interest. I will deal with the specifics of the PE approach later on.
This is all fine and dandy, but until now the PE model has focused solely on electronic molecular properties. I've extended it so you can calculate nuclear magnetic shielding constants in the PE model using London atomic orbitals (you might know them as Gauge-Including Atomic Orbitals) with contributions from charges, dipoles (induced and static) and quadrupoles. The hope is that we need a small QM region due to a very high-quality potential compared to previous QM/MM studie (see here for an example of needed more than 1000 atoms for converged NMR shieldings).
We'll see how it goes.
Apart from using DALTON instead of GAMESS I've also switched gears and I am now focused on an advanced form of QM/MM which is called polarizable embedding (see this paywalled link for details). Basically your gas-phase Fock operator is extended with interactions from the surroundings. In the language of polarizable embedding (PE) we constructs the effective Fock operator here for Hartree-Fock
$\hat{f}_{eff} = \hat{f}_{HF} + \hat{\nu}_{PE}$
The PE is a sum of interactions from the surroundings onto a molecule of interest. I will deal with the specifics of the PE approach later on.
This is all fine and dandy, but until now the PE model has focused solely on electronic molecular properties. I've extended it so you can calculate nuclear magnetic shielding constants in the PE model using London atomic orbitals (you might know them as Gauge-Including Atomic Orbitals) with contributions from charges, dipoles (induced and static) and quadrupoles. The hope is that we need a small QM region due to a very high-quality potential compared to previous QM/MM studie (see here for an example of needed more than 1000 atoms for converged NMR shieldings).
We'll see how it goes.
Subscribe to:
Posts (Atom)